連分数
こんばんは。今日もノートの投稿をします。
今週末は何をして過ごそうか悩んでいる木曜日の夜です。
みなさんは今週末は何をして過ごすか決まっていますか?
よかったらのんびりとScienceHub(サイエンスハブ)に投稿してあるノートを読んで数学や物理の勉強をして過ごすのもいいかもですね。
今日は少しあまりなじみのないものを取り上げてみます。
連分数というものです。
ご存じの方もご存じない方もよかったらお立ち寄り頂いてノートを読んでみてください。
今日ご紹介するノート
学生のころに連分数というものを知ってとても感動しました。
純粋に数学的な興味のために学生のときにプチ研究したノートの一部をまとめたものです。
面白い結果もありそうですがあまり応用例を知りません。
なじみの数式(とか)などが連分数表示されたのを見るとオッ!すげー!と思ったりしました。
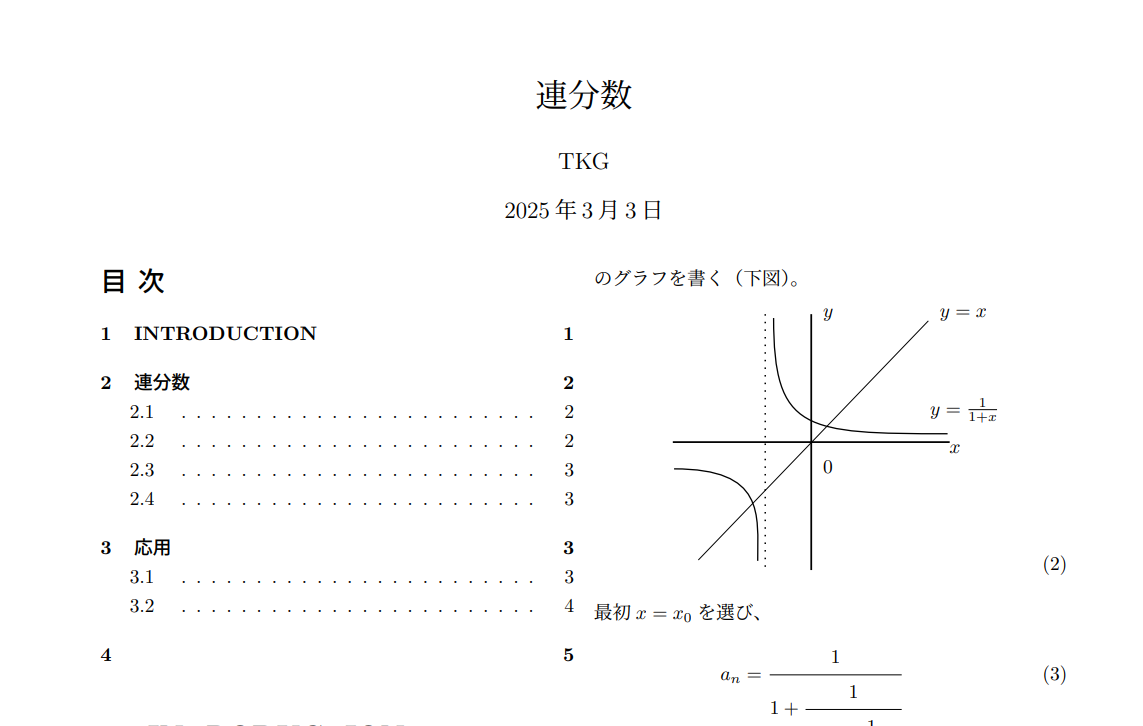
最初に紹介するのは、有名な「黄金比」の無限連分数表現。式の中に延々と同じ形が繰り返されている構造に、最初から数学的な美しさを感じてもらえると思います。
内容としては、連分数の定義やその収束の仕組みからスタートし、漸化式を使って有限連分数を効率よく求める方法、収束判定のための解析的な工夫、さらには連分数の応用として交代級数の変換法などにも触れています。や
、
といったおなじみの定数が、意外な形で連分数として表される様子を見ると、「あ、こんなところでも役に立つんだ」と思えたりします。
特に面白いのは、分母と分子の漸化式や、フィボナッチ数列とのつながり、さらには数論的な性質(分子と分母が互いに素であること)まで自然と現れてくる点。高校数学の知識があれば読み始められる内容ですが、少しずつ本格的な数学の“手触り”に触れていける構成になっています。
計算が好きな人や、美しい数式が好きな人にはぜひ読んでほしい一冊です。数学って実は、計算のテクニック以上に「構造の発見」が面白いんだ、ということを感じてもらえたら嬉しいです。
解析力学
こんにちは。ScienceHub(サイエンスハブ)運営のTKGです。
最近読んでいる物理本は英語なのですが、久しぶりに英語本読んでいてわからない単語を調べながら頑張って読み進めています。
みなさんもScienceHub(サイエンスハブ)に投稿してあるノートでまったりと勉強をしてみませんか?
今日ご紹介するノート
力学の基礎的な話題をノートにまとめました。
まずニュートン力学の復習からはじめ、剛体の運動などを解説しています。
ラグランジュ形式、正準形式、ハミルトン・ヤコビ理論あたりまで順に進めています。

この『解析力学』ノートは、わたし自身が力学の本質的な仕組み――特にニュートンからラグランジュ、ハミルトン形式、そして正準形式までの流れを一度しっかり整理してみたいと思って書いたものです。
力のベクトルで物体を追いかけるニュートン力学からスタートし、剛体の運動やエネルギー保存則、そして座標変換にも耐えるラグランジアンやハミルトニアンの枠組みへと進んでいきます。
このノートでは、力の釣り合いや仕事とエネルギー、作用の原理といった直感的なアイデアを入り口にしつつ、未定乗数法やダランベールの原理、ネータの定理のような抽象的な概念まで背景にある数学的な構造や論理の流れがわかるように順を追って扱っています。
とくにラグランジアンからハミルトニアンへのルジャンドル変換や、正準方程式、ポアソン括弧といったトピックでは、数式の意味にしっかり足を踏み入れて、「なぜそうなるのか」をできる限り自分の言葉で書くように心がけました。
「数学的にも物理的にも筋の通った力学を学びたい」「教科書に書かれていないつながりや直感を感じたい」――そんな人の一助になれば嬉しいです。保存則や対称性といった力学の“裏側”を一緒にたどっていけたらと思います。
p.s.
簡単にまとめていますが、演習問題などは含みません。
また論理展開はシンプルであることを目指しています。
数学的な厳密性よりは、直観的な理解の助けになることに重きを置いています。
みなさんの学習のご参考になれば幸いです。
ScienceHub(サイエンスハブ)では数学や物理学の学習に最適なPDFのテキストが掲載されています。
ぜひScienceHub(サイエンスハブ)に訪れてPDFのノートで学習してください。
複素解析のお話
こんにちは。ScienceHub(サイエンスハブ)の運営をしているTKGです。
今日は暑いですね。来週からは雨が降り出してまた涼しくなるみたいです。
お仕事の終わった後にでもごゆっくりとScienceHub(サイエンスハブ)のノートを見て学び直ししてみませんか?
今日ご紹介するノート
複素解析学の基本的なお話をnoteにまとめました。
複素数を扱う一般的な解析学のトピックをダイジェスト的にまとめました。

複素解析学の基本的なお話をnoteにまとめました。
複素数を扱う一般的な解析学のトピックをダイジェスト的にまとめました。
このノートは、わたしが複素解析の美しさに魅かれて、そのエッセンスをまとめておきたくなって書いたものです。
実解析の知識が少しあれば、入り口としては十分です。複素数や複素関数の定義、極限や連続性といった基本から始まり、微分可能性と正則性、そしてコーシー・リーマンの条件へと進んでいきます。
特に、正則関数の振る舞いがいかに滑らかで、制限の多い存在であるか――それがコーシーの積分定理やテイラー展開、最大値の原理、リウヴィルの定理などを通して自然に浮かび上がってくるよう意識して構成しました。
また、一般的な有理型関数の極・位数と積分の関係、無限積表示とその具体例(,
,
など)や、ベルヌーイ数・オイラー数との関連まで触れています。
難解な証明は避けつつも、数式の背景にはちゃんと踏み込んでいます。「関数が“正則”だとどうなるのか?」「積分ってなんでそんなに強力なの?」といった疑問を持った人に向けて、できるだけ自分の言葉で説明しようと努めました。
複素解析の世界の魅力の“入口”として、少しでもお役に立てばうれしいです。
以下トピックです。
- 複素数
- 複素関数
- 極限、連続性
- 微分
- 指数関数
- 積分
- コーシーの積分定理
- 正則関数の性質
- 特異点
- 有理型関数、有理型関数の級数表示例、有理型関数の無限積表示例
など
p.s.
簡単にまとめていますが、演習問題などは含みません。
また論理展開はシンプルであることを目指しています。
数学的な厳密性よりは、直観的な理解の助けになることに重きを置いています。
みなさんの学習のご参考になれば幸いです。
自己紹介 | はじめてのブログ | 実解析のお話
はじめまして。ScienceHub(サイエンスハブ)です。
このブログを見つけていただいてありがとうございます。
はじめてのブログ。
自己紹介をさせていただきます。
自己紹介
ScienceHub(サイエンスハブ)は科学系情報共有サイトで普段書き溜めている数学や物理学の学習の記録や個人の研究の記録や自作のテキストをTeXなどを用いてPDFにしてまとめている方が自由に投稿して共有できるサイトになります。
自分のテキストや研究を発信してアピールしていただけると嬉しいです!
ScienceHub(サイエンスハブ)の運営を行っているわたしの自己紹介も少しだけ。。
名前:TKG
性別:男
年齢:40代
性格:のんびり屋、楽観主義者
趣味:数学や物理学の勉強、グルメ
好きな分野:場の量子論、微分幾何、素粒子論、宇宙
投稿記事の紹介
ScienceHub(サイエンスハブ)に投稿しているノートの紹介を行っていこうと思っています。
ブログではノートの紹介だけでなく、たまに数学や物理学に関連した記事も思い付きで書いてみようと思っています。そちらもよかったらお楽しみください。
最初に紹介するノートは「実解析のお話」です。
サイトにPDFを公開していますのでよかったらサイトに訪れてみてもらえると嬉しいです。
実解析のお話

解析学の基本的なお話をnoteにまとめました。
実数を扱う解析学、あるいは微分積分のトピックをダイジェスト的にまとめました。
このノートは、わたしが実解析の基礎をもう一度きちんと整理しようと思ってまとめたものです。
高校や大学初年次で習う微分・積分でなんとなく「公式を使う」だけで済ませていませんか?
それらが本当はどういう意味を持っているのか、を改めて考える材料になるといいなと思います。
最初は数列や関数の極限、連続性の定義から始まり、そこから順を追って微分、積分、級数、関数列と進んでいきます。
証明というよりは、「どうしてそうなるのか」「それってつまり何を言ってるのか」を意識して書きました。
なので、ある程度の数式にはなじみがあるけど、ちょっとモヤモヤしている人には、ちょうどいい整理になるかもしれません。
また、多変数関数やテイラー展開、関数列の収束、一様収束の話も入れてあります。理工系の学生が大学後半で悩みがちなポイントにも軽く触れていて、「ふわっとしていた理解が少しずつ輪郭を持ってくる」ような感覚を大事にしました。
難解な定理や厳密な証明はあえて避けていますが、数式の使い方や導き方にはある程度こだわったつもりです。
「解析をちゃんと理解したいけど、教科書はちょっと硬すぎる…」という人の手がかりになれば嬉しいです。
以下トピックです。
p.s
簡単にまとめていますが、演習問題などは含みません。
論理展開がシンプルであることを目指しています。
数学的な厳密性よりは、直観的な理解の助けになることに重きを置いています。
みなさんの学習のご参考になれば幸いです。